서포트 벡터 머신SVM(support vector machine)
서포트 벡터 머신은 선형, 비선형 분류, 회귀, 이상치 탑색에도 사용가능한 다목적 모델이다.
복잡한 분류 문제에 잘 맞으면 중소 크기의 데이터셋에 적합하다.
5.1 선형 SVM 분류
선형 SVM분류기는 두개의 클래스를 하나의 직선으로 분류할때, 결정 경계에 제일 가까운 훈련 샘플로부터 가능한 멀리 떨어지도록 결정 경계를 생성한다. 즉 가장 폭이 넓은 도로를 찾는 것과 같다. 이를 라지 마진 분류large margine classification 이라고 한다. 도로 경계 또는 안쪽에 위치한 샘플들에 의해 전적으로 결정(의지)된다. 이런 샘플을 서포트 벡터support vector 라고 한다.
5.1.1 소프트 마진 분류
모든 샘플이 도로 바깥에 올바르게 위치할 경우 하드 마진 분류hard margine classification 이라고 한다.
문제점 : 데이터가 선형적으로 구분될 수 있어야 제대로 작동한다, 이상치에 민감하다.
도로폭을 가능한 넓게 유지하는것과 마진 오류의 균형을 잡은 유연한 모델이 소프트 마진 분류soft margine classification 이다.
5.1.2 비선형 SVM 분류
선형적으로 분류할 수 없는 많은 비선형 데이터 셋에는 다항 특성과 같은 특성을 더 추가하는 것이다.
5.2.1 다항식 커널
다항식 특성을 추가하는 것은 간단하지만, 낮은 차수의 다항식은 잘 표현이 안되고, 높은 차수의 다항식은 많은 특성수를 필요로해 느리다.
SVM을 사용할때는 커널 트릭kernel trick이라는 수학적 기교를 적용한다.
커널 트릭은 실제로 특성을 추가하지 않으면서 다항식 특성을 추가한 결과를 가질 수 있다.
5.2.2 유사도 특성
비선형 특성을 다룰 때 각 샘플이 특정 랜드마크landmark와 얼마나 닮았는지를 측정하는 유사도 함수similarity function로 계산한 특성을 추가한다.
유사도 함수를 가우시안 방사 기저 함수radial basis function 라고 정의하면,
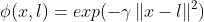
이 함수의 값은 랜드마크에서 매우 멀리떨어질때 0, 랜드마크와 같은 위치(x = l)일때 1 까지 변화하며, 종모양으로 나타난다. 각 샘플들의 함수값을 도출해서 새로운 특성을 만들어낸다.
랜드마크를 선택하는 간단한 방법은 데이터셋에 있는 모든 샘플 위치에 랜드마크를 지정하여, n개의 특성을 가진 m개의 샘플이 있을경우, m개의 특성을 가진 m개의 샘플로 변환된다. (원래 n개의 특성은 제외라고 가정한다.) 훈련세트가 클경우 동일한 크기위 아주 많은 특성이 만들어진다.
5.2.3 가우시안 RBF 커널
유사도 특성 방식도 다항 특성 방식과 마찬가지로 머신러닝 알고리즘에 유용하게 사용될 수 있다.
훈련 세트가 클 경우, 추가 특성 계산에 연산 비용이 많이드는데 이때 커널 트릭이 다시한번 사용된다.
유사도 특성을 많이 추가하는 것과 비슷한 결과를 얻을 수 있다.
감마 값이 클수록 종모양이 좁아져 랜드마크가 샘플 좁은 범위에 영향을 주어 결정 경계가 조금 더 불규칙 해지고, 샘플을 따라 구불구불하게 휘어진다. 감마 값이 작을수록 샘플 넓은 범위에 영향을 주어 결정 경계가 더 부드러워진다. 즉 감마 값이 규제 역할을 한다.
문자열 커널도 가끔 사용된다. 문자열 서프시퀀스 커널, 레벤슈타인 거리 기반의 커널 등..
커널 종류 선택방법? : 경험적으로 선형 커널을 가장 먼저 시도해본다. 훈련 세트가 아주 크거나, 특성수가 많을때. 훈련 세트가 적당하다면 가우시안 RBF 커널도 시도해보고, 교차 검증과 그리드 탐색을 통해 다른 커널도 사용가능하다.
5.3 SVM 회귀
SVM은 분류 뿐아니라 선형, 비선형 회귀에도 사용가능하다.
목표를 반대로 하여 제한된 마진오류(도로 밖의 샘플) 안에서 도로안에 가능한 한 많은 샘플이 들어가도록 학습한다.
도로의 폭은 하이퍼파라미터 epsilon으로 조절한다. 마진안에서 훈련샘플이 추가되어도 모델의 예측에 영향이 없는 이 모델을 epsilon-insensitive라고 한다.
비선형 회귀작업에는 커널 SVM 모델을 사용한다.
5.4 SVM 이론
표기법 : Theta = 편향과 가중치 n개의 모델파라미터를 모두 합친 벡터
b = 편향
w = 가중치 벡터
5.4.1 결정 함수와 예측
선형 SVM 분류기 훈련 알고리즘은 w.T x + b = w1x1 + w2x2 + ... + wnxn 을 계산해서 0보다 크면 예측 클래스 y_hat이 1 작으면 y_hat이 0 으로 예측한다.
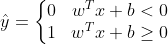
특성이 2개있는 데이터셋에는 결정함수가 2차원 평면으로 나타난다. 결정 경계는 결정함수가 0 인 직선이다. 두 평면(결정함수, 데이터셋)의 교차점으로 나타난다.
결정 경계에 나란하고 일정 거리만큼 떨어져 마진을 형성하는 직선 2개는, 결정 함수의 값이 1과 -1 인 직선이다.
선형 SVM분류기를 훈련하는 것은 마진 오류를 하나도 발생하지 않거나(하드 마진) 제한적인 마진 오류를 가지면서(소프트 마진)가능한 한 마진을 크게하는 가중치벡터(w)와 편향(b)를 찾는 것이다.
5.4.2 목적 함수
결정함수의 기울기는 가중치벡터의 l1노름과 같다. 결정함수의 기울기가 2배 감소하면 마진은 2배 증가한다. 즉, 가중치 벡터가 작을수록 마진은 커진다.
마진을 최대화하기 위해서 가중치벡터의 노름을 최소화하려고한다. 마진 오류를 하나도 만들지 않기 위해서(하드마진) 모든 양성 훈련샘픔의 함수값이 1보다 커야하고, 음성 훈련 샘플은 -1 보다 작아야 한다.
따라서 t 를 음성샘플일때 -1, 양성샘플일때 1 이라고 정의하면 목적함수를 정의할 수 있다.
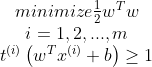
소프트 마진 분류기에서 목적 함수를 구성하려면 각 샘플에 대해 슬랙 변수slack variable 을 도입한다. 이 변수는 i 번째 샘플이 얼마나 마진을 위반할 지 정한다. 즉 샘플이 마진을 최대로 위반할 정도를 정한다.
이 문제는 두개의 상충되는 목표를 지닌다.
하나는 마진오류를 최소화 하기 위해 가능한 한 슬랙 변수(zeta로 표기)를 최소화해야하고,
하나는 마진을 최대화 하기위해서 1/2||w||^2를 가능한 작게 만드는 것이다.
여기에 하이퍼 파라미터 C를 도입해 상충되는 두 목표사이 트레이드 오프를 정의한다.
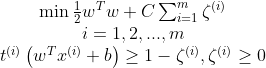
5.4.3 콰드라틱 프로그래밍
하드 마진과 소프트 마진의 선형적인 제한조건이 있는 볼록함수의 이차 최적화 문제는 콰드라틱 프로그래밍(QP)문제 라고한다.
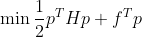
조건 : Ap <= b
p 는 n_p 차원의 벡터( n_p = 모델 파라미터 수)
H는 n_p X n_p 크기 행렬
f 는 n_p 차원의 벡터
A는 n_c X n_p 크기 행렬(n_c = 제약 수)
b는 n_c 차원의 벡터
Ap <= b는 n_c개의 제약을 정의한다. (위에서 zeta로 나타난 각 슬랙 변수)
i = 1 , ... , n_c 일때, p^T a^(i) <= b^(i) 인 제약이 있다. a^(i)는 A의 i번째 행의 원소, b^(i)는 b의 i번째 원소
QP파라미터를 지정하면 선형 SVM 분류기의 목적 함수를 간단한게 검증할 수 있다.
n_p = n + 1 (특성 수 + 편향)
n_c = m (m = 훈련 샘플 수)
H : n_p X n_p 크기, 맨 왼쪽위 원소가 0 인 단위 행렬이다. (편향을 제외하기 위해)
f = 0. 모두 0 으로 채워진 n_c 차원의 벡터
b = 1 모두 1로 채워진 n_p 차원의 벡터
a^(i) = -t^(i)x^(i) , x'^(i)는 편향을 위해 x^(i)에 특성 x'_0 = 1을 추가한 벡터
하드 마진의 경우 이미 만들어진 QP알고리즘에 관련 파라미터를 전달하기만 하면된다.
커널 트릭을 사용하려면 제약이 있는 최적화 문제를 다른 형태로 바꿔야한다.
5.4.4 쌍대 문제dual problem
원 문제primal problem 라는 제약이 있는 최적화 문제가 주어지면, 쌍대 문제dual problem라고하는 깊게 관련된 다른 문제로 표현 가능하다. 일반적으로 쌍대 문제 해는 원 문제의 하한값이지만, 어떤 조건하에 동일한 해를 제공한다.
SVM은 이 조건을 만족해서 원 문제와 쌍대문제가 동일한 해를 가져 선택해서 풀 수 있다.
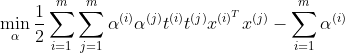
이 식을 최소화하는 벡터 alpha로 원 문제의 식을 최소화하는 w와 b를 얻을 수 있다.
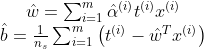
훈련 샘플 수가 특성 개수보다 작을 때 쌍대 문제를 푸는 것이 더 빠르다. 이때 중요한 것은 원문제에선 적용이 안되는 커널 트릭을 가능하게 한다.
5.4.5 커널 SVM
2차원 데이터셋에 2차 다항식 변환을 적용하고 SVM 분류기에 적용한다고 할때, 다항식 매핑함수 Phi를 도입한다.
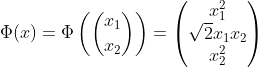
변형된 벡터는 3차원이 되고, 2개의 2차원 벡터 a,b를 Phi에 적용후 점곱(dot product)을 하면, 원래 벡터의 점곱의 제곱과 같다.
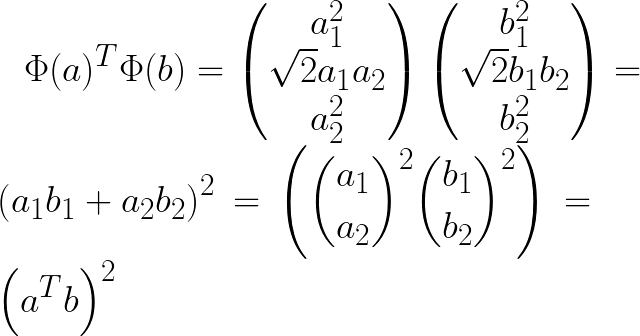
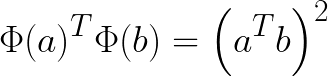
핵심은 모든 샘플에 Phi함수를 적용시키면 위의 쌍대 문제의 목적함수에서 x의 i, j의 점곱항이 점곱의 제곱항으로 변환된다. 그런데 여기서 훈련샘플을 변환시킬 필요없이, 점곱을 제곱으로 바꿔주기만하면 된다. 그 결과값은 어렵게 모든 샘플을 Phi함수를 적용시켜 변환한 뒤 선형 SVM알고리즘을 적용하는 것과 완전히 동일하기 때문이다.
함수 K(a, b) = (a.T b)^2을 2차 다항식 커널 이라고 부른다. 머신러닝에서 커널은 변환 Phi를 모르더라도, 원래 벡터 a b 에 기반하여 점곱의 제곱을 계산할 수 있는 함수이다.

[[머서의 정리
Phi함수가 존재하는지 여부를 확인하기 위해서 머셔의 정리를 사용한다.
K(a,b)가 머셔의 조건라 부르는 몇개의 조건을 만족하면, K(a,b) = Phi(a).T Phi(b)를 만족하는 함수 Phi가 존재한다.
따라서 Phi를 모르더라도 존재여부는 알기 때문에, K를 커널로 사용 가능하다.
가우시안 RBF 커널의 경우 Phi는 각 훈련 샘플을 무한 차원 공간에 매핑한다.
자주 사용하는 일부 커널(ex 시그모이드)의 경우 머서의 조건을 모두 만족하지는 않지만 일반적으로 실전에서 잘 작동한다.]]
위의 커널을 사용하여 쌍대문제의 alpha를 얻어서 원문제를 풀기 위해서는 결국 예측식에 Phi(x^(i))를 포함해야 한다.
w_hat을 구할때, w_hat의 차원은 매우 크거나 무한한 Phi(x^(i))의 차원과 같아져야 하므로 이를 계산할 수 없다.
하지만 예측식을 변형해서 입력벡터간의 점곱으로 나타낼 수 있다.
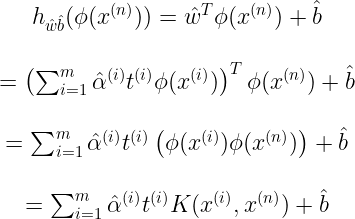

5.4.6 온라인 SVM
온라인 학습은 새로운 샘플이 생겼을때, 점진적으로 학습하는 것을 말한다.
온라인 SVM 분류기를 구현하는 한가지 방법은 원 문제로부터 유도된 비용함수를 최소화 하기 위한 경사하강법을 사용하는 것이다. 하지만 경사 하강법은 QP 기반의 방법 보다 훨씬 느리게 수렴한다.
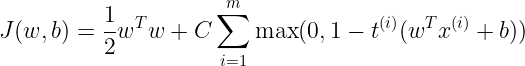
첫항은 작은 가중치 벡터 w(기울기)를 가지도록 제약을 가해 마진을 크게만든다.
두번째 항은 마진 오류를 계산한다. 올바르지 않은 방향으로 벗어난 거리에 비례한다.
[[ 힌지 손실 ]]
max(0, 1-t) 함수를 힌지 손실hinge loss 함수라고 부른다. 위에서도 힌지손실함수가 씌였다.
t = 1 에서 미분가능하지 않지만, 서브그레디언트를 사용해 경사 하강법을 사용할 수 있다. (즉 -1 ~ 0 사이 값을 이용)